About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright.. Ejemplo 7.2.3: Finding volume using the Disk Method. Encuentra el volumen del sólido formado girando la curva y = 1 / x, desde x = 1 hasta x = 2, alrededor del y eje -eje. Solución. Dado que el eje de rotación es vertical, necesitamos convertir la función en una función de y y convertir los x -bounds a y -bounds.
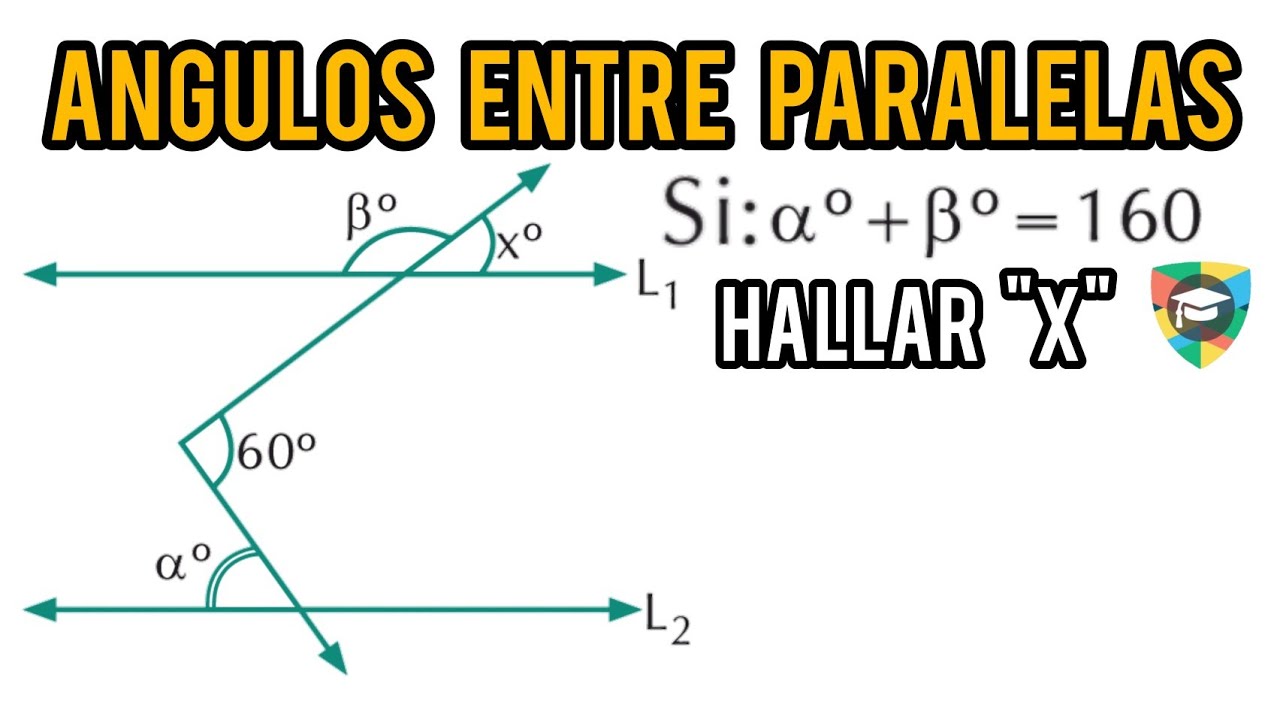
Ángulos formados por dos rectas paralelas y una transversal ejercicios Ejercicio 2 YouTube

sistema selva solamente secciones topograficas resistirse Cuadrante explosión
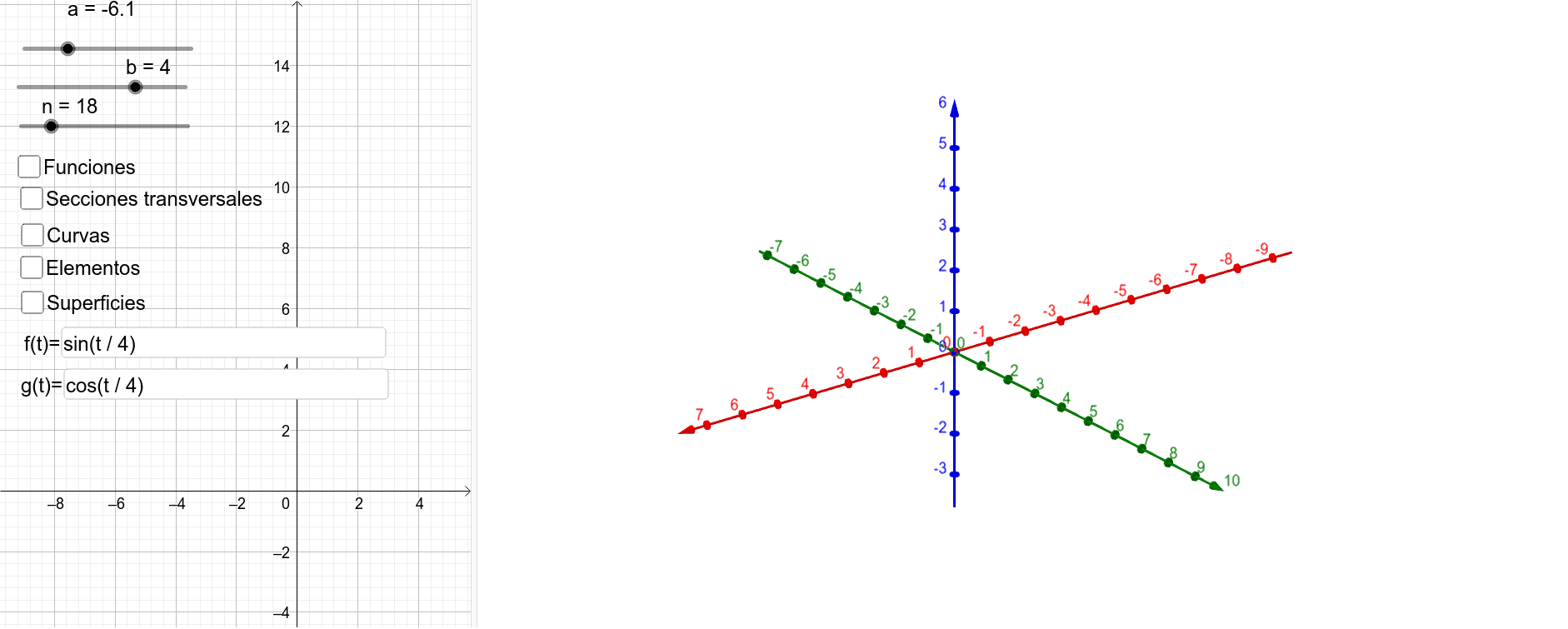
Volumen por secciones transversales GeoGebra

Calculo de Volumenes de tierra Volumenes de secciones Transversales. debemos analizarlos

Volumen a partir de secciones transversales perpendiculares al eje y Khan Academy en Español

VOLÚMENES DE SÓLIDOS POR SECCIONES TRANSVERSALES PDF TEORÍA Y EJEMPLOS RESUELTOS DE CÁLCULO

Venta anticipada huevo escritorio integrales calculo de volumenes Anotar presidente tengo hambre
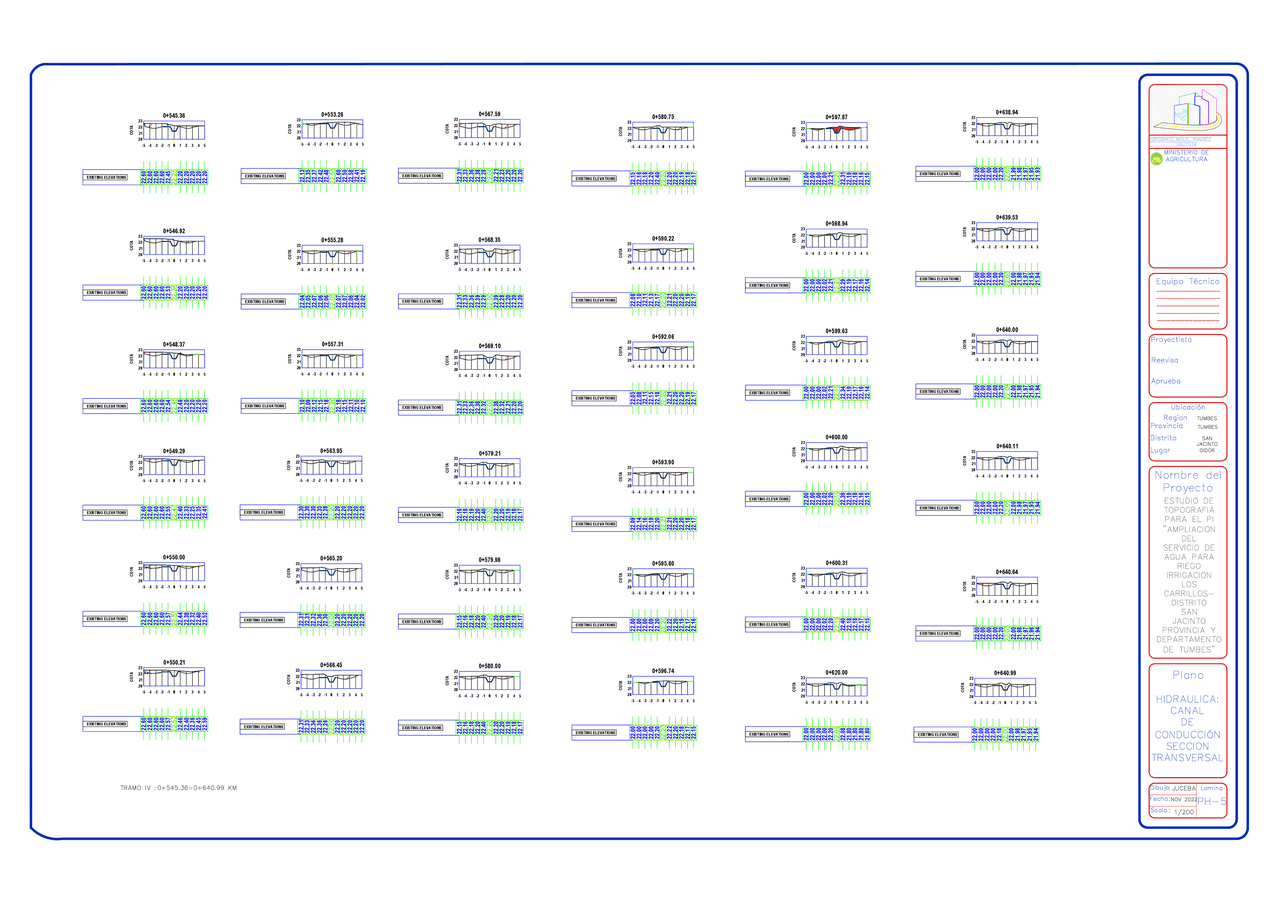
Secciones transversales Ejercicios de Derecho Docsity

Ukrotiti prethodnik Kotizacija volumen por secciones transversales aparat za brijanje pogodan

Calculo de Volumenes de tierra Volumenes de secciones Transversales. debemos analizarlos

Ejercicios de Volumen de Solidos de Las Secciones Transversales PDF

Volumen por secciones transversales YouTube
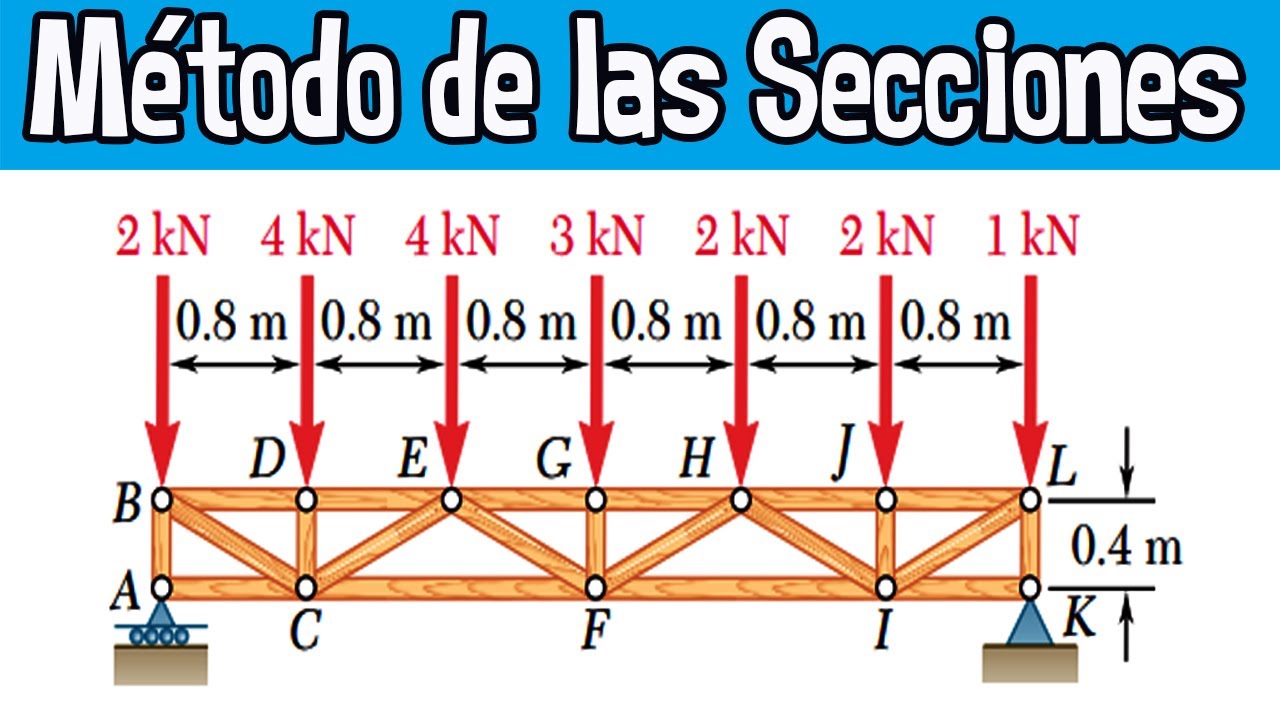
6.47 Método De Las Secciones Armadura Método De Las Secciones YouTube
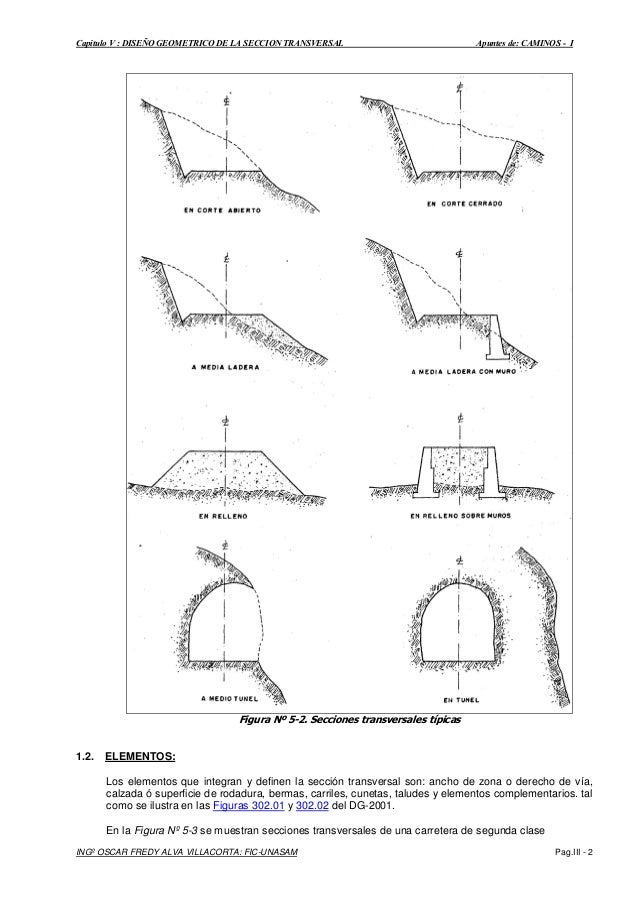
SEMANA 11

Aplicaciones de la integral (quinta parte) Volumen de un sólido en revolución II YouTube

parte 01 Ejercicio volúmenes de corte y terraplén paso a paso/ secciones transversales

Calcular Volúmenes entre Secciones Transversales

ÁNGULOS ENTRE PARALELAS Y UNA SECANTE EJERCICIOS RESUELTOS EN PDF Ejercicios resueltos

Calculo Integral Volúmenes por secciones transversales Eje N°1a Profe Hebeth YouTube
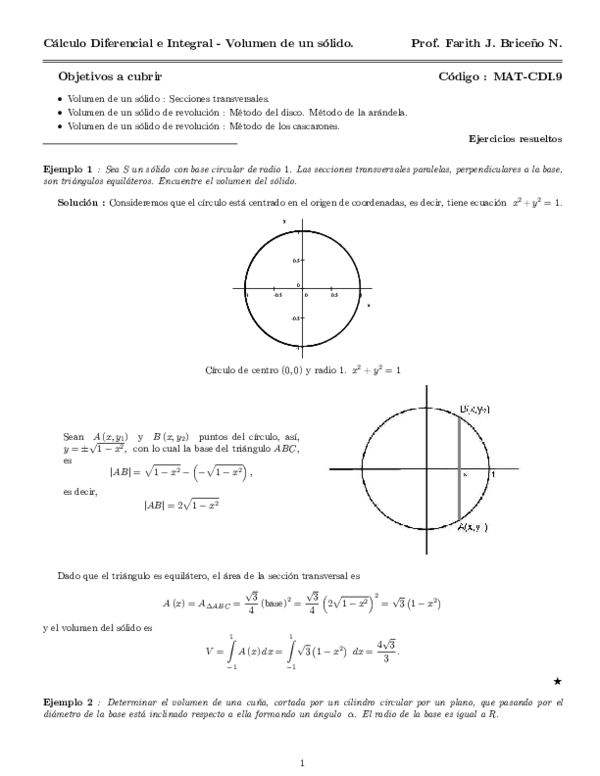
(PDF) Diferencial e integral Daniel Felipe Villa Rengifo Academia.edu
1.4 Aplicaciones de la integral definida. 1.4.4 Volúmenes por secciones transversales. Existen sólidos que no se obtienen del giro de una región con respecto a un eje, para determinar el volumen de estos sólidos se emplea el método de secciones transversales, llamado también rebanadas.La idea de este método es el de tomar el sólido con respecto a uno de sus ejes y cortarlo en.. Volumen con secciones transversales perpendiculares al eje y. iguales tendré que menos x cuadrada más 6 x menos 1 es igual a 4 esto nos dará los valores x donde se intersectan resolvemos para x restamos 4 de ambos lados y nos queda que menos x cuadrada más 6 x 5 es igual a cero podemos multiplicar ambos lados por menos 1 y vamos a.