Two unpaired t tests. When you choose to compare the means of two nonpaired groups with a t test, you have two choices: •Use the standard unpaired t test. It assumes that both groups of data are sampled from Gaussian populations with the same standard deviation. •Use the unequal variance t test, also called the Welch t test.. The Welch t Test is also known an Unequal Variance t Test or Separate Variances t Test. No outliers; Note:. Note that this form of the independent samples t test statistic assumes equal variances. Because we assume equal population variances, it is OK to "pool" the sample variances (s p). However, if this assumption is violated, the pooled.

Introduction to ttests (statistics)

PPT Comparison of two samples PowerPoint Presentation, free download ID755904

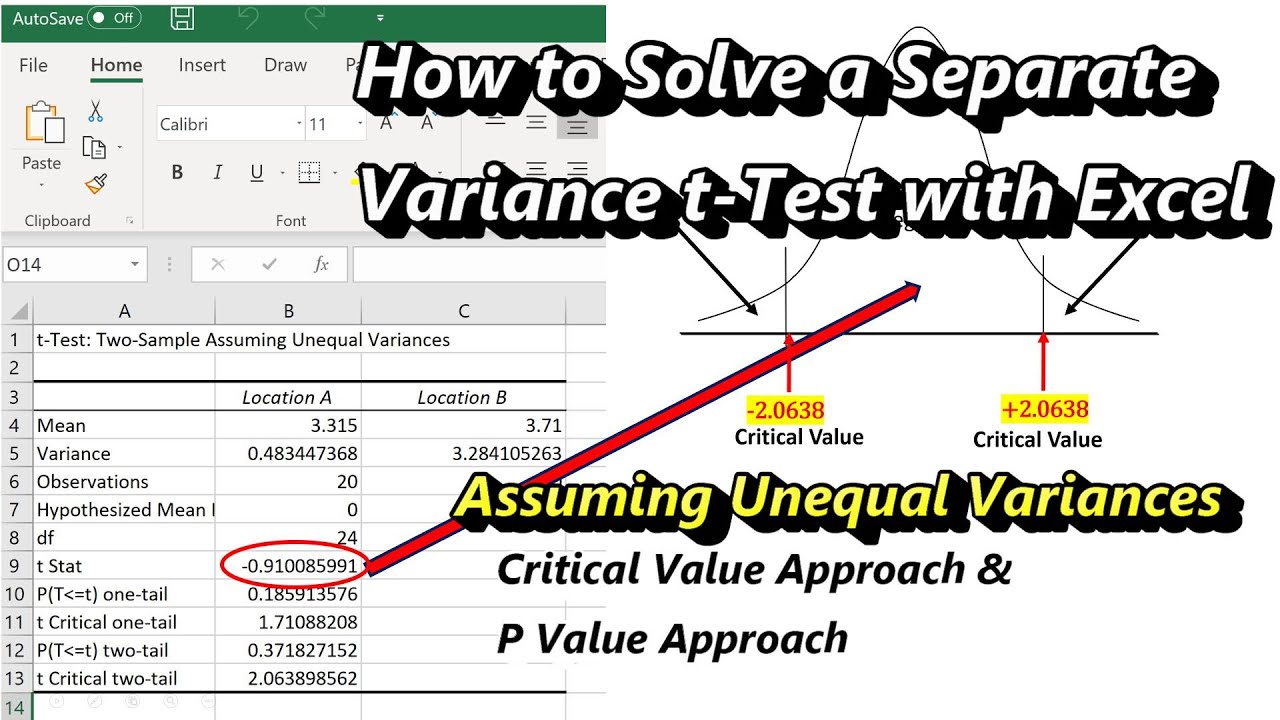
TTest for Unequal Variances Using Excel Comparing the Means of Two Independent Populations

FTest for Equality of Two Variances Quality Gurus

Equalvariance (A) and unequalvariance (B) SDT models, and the... Download Scientific Diagram

Two sample unequal variance t test wescount

T Test Example

Two sample t test equal variances assumed

Two Sample t Test (Independent Samples) Quality Gurus

PPT Classical Hypothesis Testing Theory PowerPoint Presentation, free download ID545319

PPT Analysis of Variance PowerPoint Presentation, free download ID706835

PPT STA 291 Summer 2010 PowerPoint Presentation, free download ID2441268

PPT T Tests Comparison of Means PowerPoint Presentation, free download ID5567404

Using Excel for a Pooled Variance Ttest with Equal Variances Two Population Means Sigma

PPT Module 27 Two Sample ttests With Unequal Variances PowerPoint Presentation ID781852

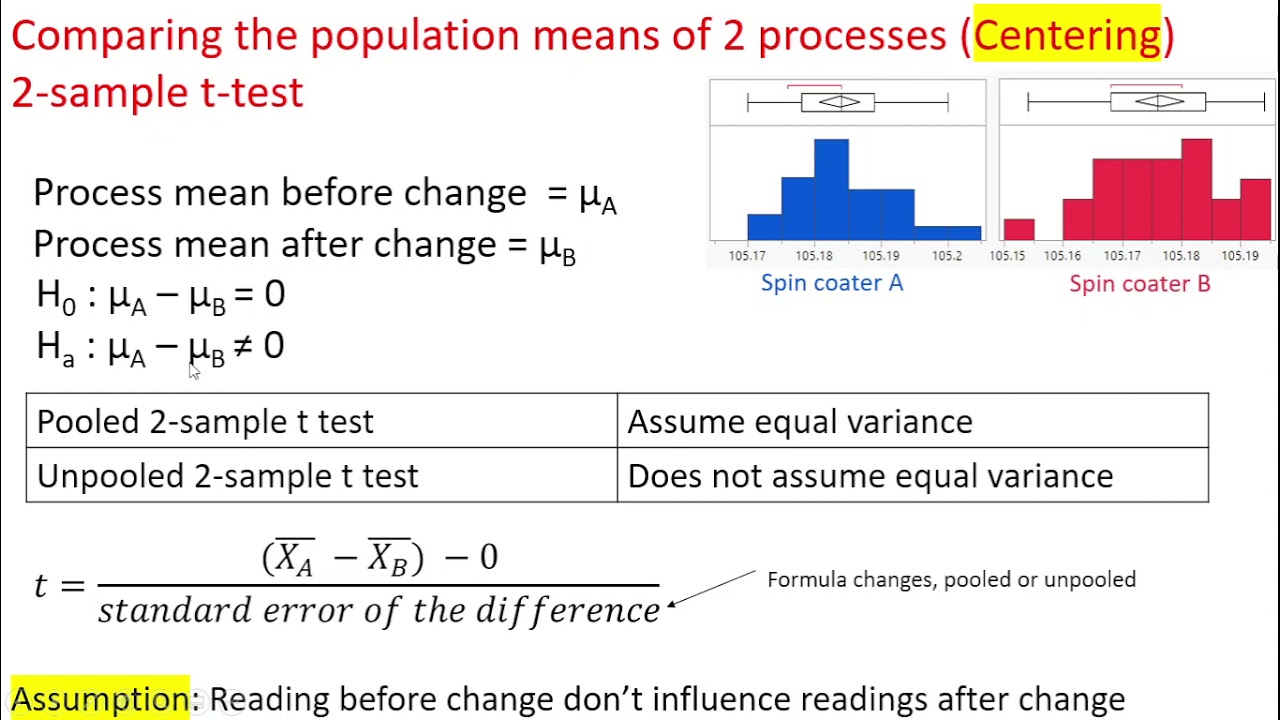
Hypothesis testing Comparing 2 processes using unequal variance test and 2sample t test JMP

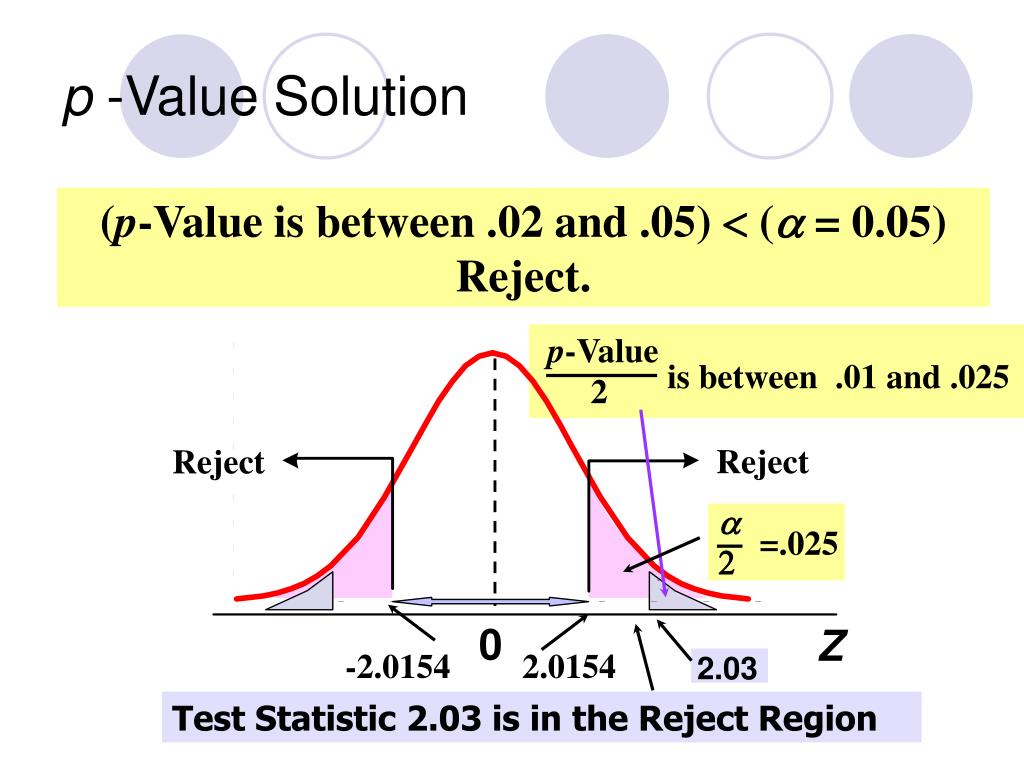
T Test Two Sample Assuming Equal Variances Example

PPT Module 27 Two Sample ttests With Unequal Variances PowerPoint Presentation ID781852

what is the correct ttest to use? Cross Validated

PPT ENGR 610 Applied Statistics Fall 2007 Week 8 PowerPoint Presentation ID790316

Many statistical procedures, such as analysis of variance (ANOVA) and regression, assume that although different samples can come from populations with different means, they have the same variance. Because the susceptibility of different procedures to unequal variances varies greatly, so does the need to do a test for equal variances.. The t test assumes your data: are independent; are (approximately) normally distributed; have a similar amount of variance within each group being compared (a.k.a. homogeneity of variance) If your data do not fit these assumptions, you can try a nonparametric alternative to the t test, such as the Wilcoxon Signed-Rank test for data with unequal.