I punti di non derivabilità di una funzione si dividono in punti angolosi, punti di cuspide e punti di flesso a tangente verticale e sono punti in cui la funzione è continua ma non derivabile. Per determinarli, bisogna calcolare il limite del rapporto incrementale o il limite della derivata prima per x che tende a questi valori, che.. Se f'(x_0) = 0 allora x_0 è detto più propriamente punto di flesso a tangente orizzontale. Dal punto di vista geometrico, dato un punto di flesso x_0 il grafico della funzione f attraversa la retta tangente al grafico stesso nel punto. Teorema (caratterizzazione dei punti di flesso con la derivata seconda) Sia f è derivabile due volte in un.
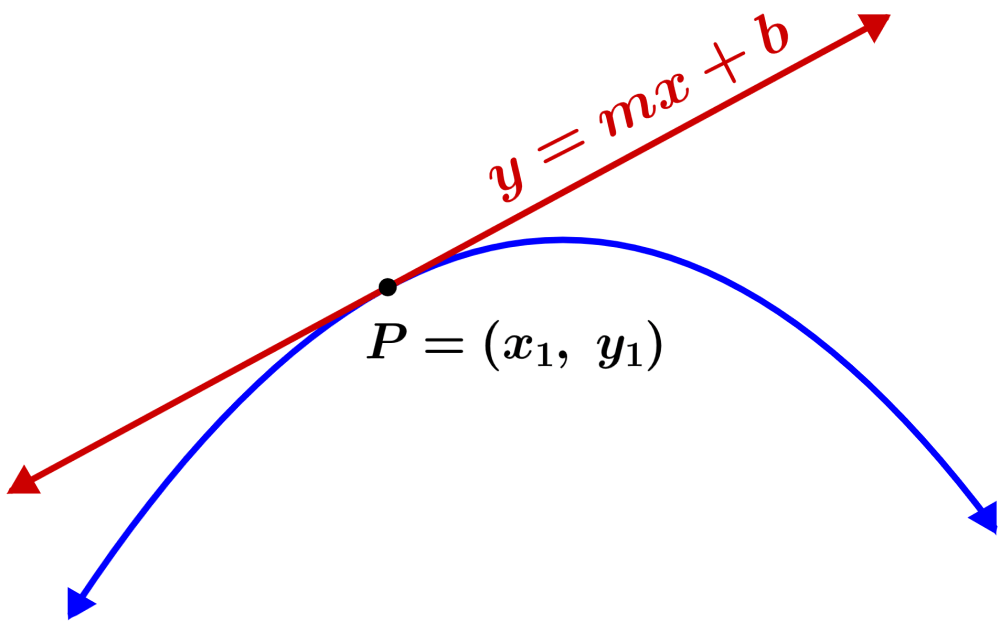
Recta tangente y recta normal a una curva Fórmulas y ejemplos Neurochispas

Punti di non derivabilità Punti angolosi, cuspidi, flessi a tangente verticale Matepensa

Punti di non derivabilità dalla cuspide al punto angoloso Studenti.it
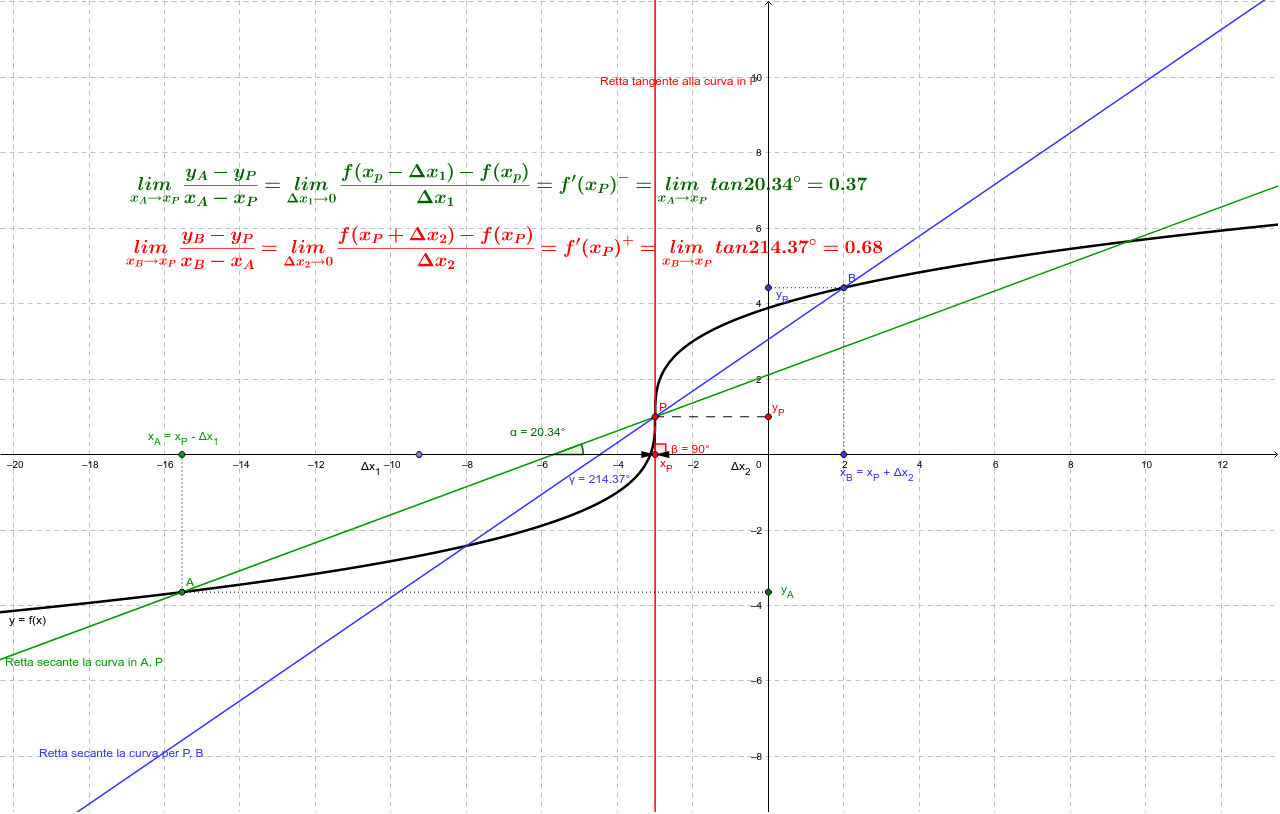
Punto di Flesso a tangente verticale GeoGebra

Punti di non derivabilità dalla cuspide al punto angoloso Studenti.it

Classificazione e studio dei punti di non derivabilità. Matematica quarta superiore

SOLUTION Punto angoloso flesso a tangente verticale cuspide teoria Studypool
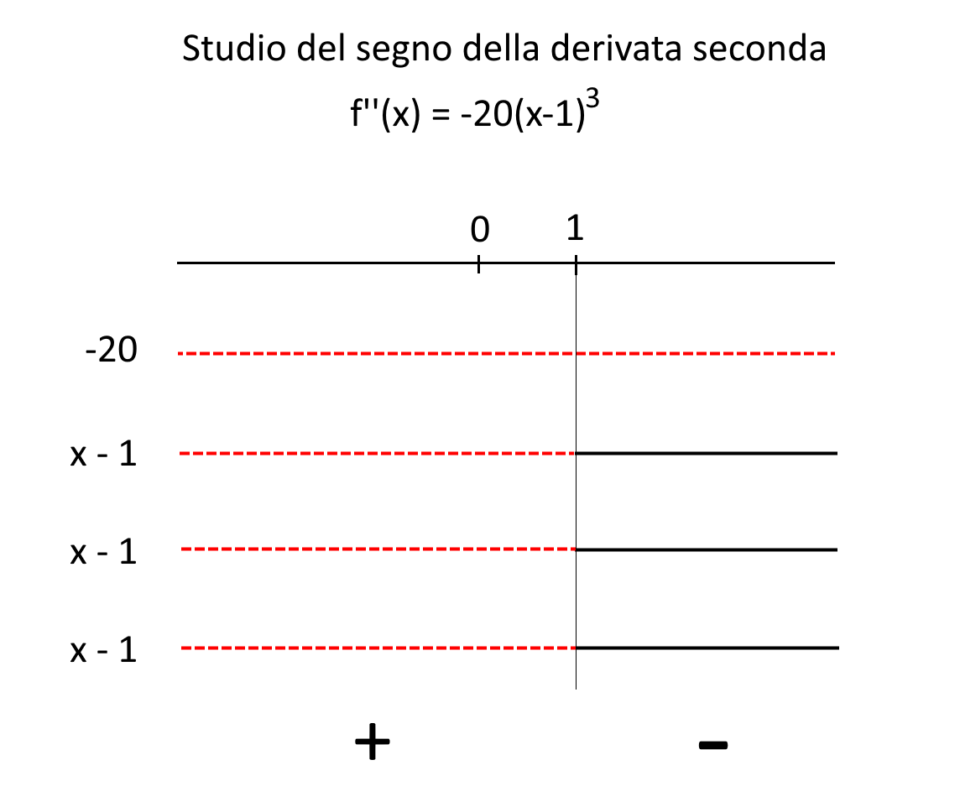
Definizione di punto di flesso (con regole per i punti di flesso) Altramatica

Studio di funzione non derivabile .Cuspide , flesso a tangente verticale YouTube

Punti di non derivabilità (punti angolosi, cuspidi, flessi a tangente verticale) YouTube

GEOGEBRA Files Flessi a tangente verticale YouTube

Punti di non derivabilità Cuspidi , Flessi a Tangente Verticale e Punti Angolosi YouTube

SOLUTION Punto angoloso flesso a tangente verticale cuspide teoria Studypool
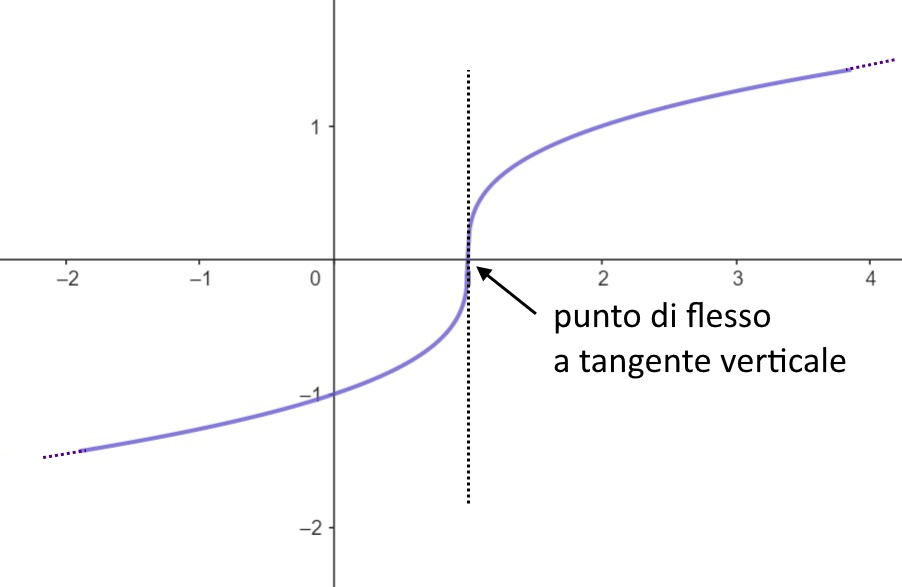
MASSIMI e MINIMI 20 esercizi SVOLTI ! MondoFisica.it

Punti di flesso a tangente verticale YouTube

PUNTI di NON DERIVABILITA' punti di flesso a tangente verticale YouTube

PUNTI DI NON DERIVABILITA' (flesso a tangente verticale, punto angoloso e cuspide) YouTube

flesso in "Enciclopedia della Matematica"
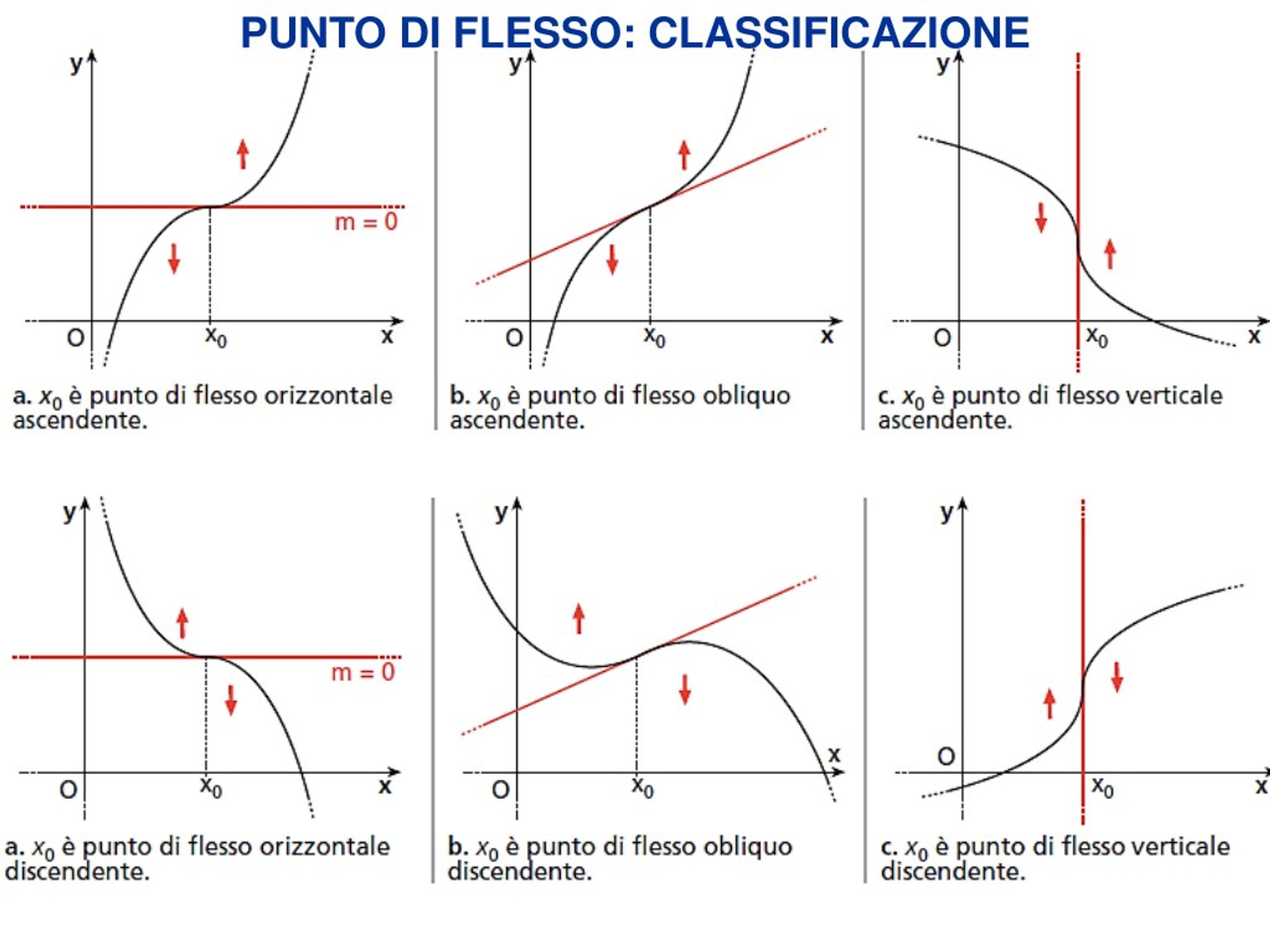
PPT bdsdf PowerPoint Presentation, free download ID8119077

Punto di flesso a tangente verticale » Esercizi svolti di Matematica e Fisica
Per il riferimento a tutte le lezioni di fisica consultare:IL MIO LIBRO DI FISICA su questo link : https://docs.google.com/document/d/1iPpiKvvGeCq5UBNyYvgMEY.. Punti di non derivabilità: cuspide, punto di flesso e punto angoloso. Abbiamo visto che cos'è la derivata di una funzione. Ma come si fa a stabilire se una funzione f f sia derivabile o meno in un dato punto x_0 x0 del proprio dominio? La derivata è il limite del rapporto incrementale. Tale limite può esistere o non esistere.